We now introduce the idea that the metric acts as a
mapping between vectors and one- forms.
To see how this works, consider 
and a single vector 
.
Since the metric requires two vectorial arguments,
the expression 
still lacks
one: when another one is supplied, it becomes a number.
Therefore can be considered as a linear function of vectors producing
real numbers: a one- form. We call it 
.
So we have
Then is a one- form whose value on a vector 
is
:
What are the components of 
. They are
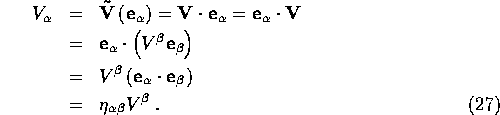
Thus
and
This can be summarized as follows: If
then
The components of are obtained from those of
by changing the sign of the time component.
Since 
[ i.e. non zero ], there
exists an inverse metric which we can write as 
[ In
Special Relativity the components of 
are the same as
, but this will not be true in the curved
spacetime of General Relativity ].
The inverse metric defines a map from one- forms to vectors
In particular, we can map the gradient one- form 
into
a vector gradient :
We can regard a vector as a 1/0 tensor i.e. a map from one- forms into the reals, so
and
The inverse metric can be used to define the magnitude
of a one- form :
and the scalar product of two one- forms :
These are identical to the corresponding quantities for vectors, i.e.
Thus one- forms are timelike/spacelike/null
if the corresponding vectors are .